TDigest 算法原理
作者: 康凯森
日期: 2017-06-22
分类: 算法
Kylin 2.0支持了近似百分位函数,是基于TDigest实现的,兴趣使然,就阅读了TDigest的论文和代码。
这是我分享的PPT: http://blog.bcmeng.com/pdf/TDigest.pdf
建议PPT和下面的补充说明结合着看,应该就可以理解TDigest算法。
TDigest是一个简单,快速,精确度高,可并行化的近似百分位算法,被Spark,ES,Kylin等系统使用。TDigest主要有两种实现算法,一种是buffer-and-merge算法,一种是聚类算法。
插值是通过已知的离散数据求未知数据的过程或方法,线性插值是最简单的插值算法。
TDigest算法的核心思想是Sketch,Sketch的直译是素描。我们这里的Sketch是一种抽象,一种简化的思想,一种处理问题的方式。Sketch其实十分常见,比如统计学中的均值和方差,物理学中的质量,密度。个人认为Sketch具有两个重要特点:1 Sketch就意味着全量数据是有丢弃的,原始的信息是有损失的。 2 Sketch后保留下来的是在特定场景或者应用下,我们关心的原始数据的特征和维度。TDigest算法使用的具体的Sketch的方法就是质心。
两种TDigest算法估计具体的百分位数时,都是根据百分位数对应的两个质心去线性插值计算的,和精准百分位数的计算方式一样。
如何根据质心估算分位数
当我们有了几百个离散的质心后,我们如何根据质心来计算任意的百分位值呢? 答案是插值
首先我们根据百分位q和所有执行的总权重计算出index; 其次找出和对应index相邻的两个质心; 最终可以根据两个质心的均值和权重用插值的方法计算出对应的百分位数。(实际的计算方法就是加权平均)
由此我们可以知道,百分位数q的计算误差要越小,其对应的两个质心的均值应该越接近。
TDigest算法的关键就是如何控制质心的数量,质心的数量越多,显然估计的精度就会越高,但是需要的内存就会越多,计算效率也越低;但是质心数量越少,估计的精度就很低,所以就需要一个权衡。TDigest算法特意优化了q=0和q=1附近的百分位精度,通过专门的映射函数K保证了q=0和q=1附近的质心权重较小,数量较多。
TDigest构建算法1 buffer-and-merge
这个算法的核心思想比较简单: 将新加入的point加入tmp buffer中,当tmp buffer满了或者需要计算quantile时,将tmp buffer中的point和已经merge的质心一起排序。(其中point和质心的表达方式是完全一样的:(mean,weight),每个point的men就是其本身,weight默认是1)。然后遍历所有的point和质心,满足merge条件的point和质心就进行merge,生成新的质心。
那么现在的关键问题就是对于排序后每个point,我们如何判断是应该加入并更新当前质心,还是新建一个质心呢? 注意:point已经有序
简单来讲,假设我们有200个质心,那么我们就可以将0到1拆分200等份,则每个质心就对应0.5个百分位。假如现在有10000个点,即总权重是10000,我们按照大小对10000个点排序后,就可以确定每个质心的权重(每个质心代表的point的个数,一般每个point的权重默认为1)应该在10000/200 = 500左右,所以说当每个质心的权重小于500时,我们就可以将当前point加入当前的质心,否则就新建一个质心。
这样的确是可行的,但是在实际应用中,我们一般更加关心90%,95%,99%等极端的百分位数,所以我们希望在q=0或者q=1附近的质心权重可以小一些,质心数量更多一些,q=0.5附近的质心权重可以大一些,质心数量更少一些。 这样做的好处是可以让q=0或者q=1附近的百分位估计精度更高。
我们令k表示百分数q应该对应第k个质心,则在我们简单做法中k和q之间的映射函数就是k=compression*q。而TDigest实际使用的映射函数如下:
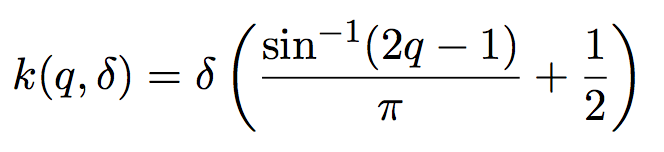
对应的函数图像如下
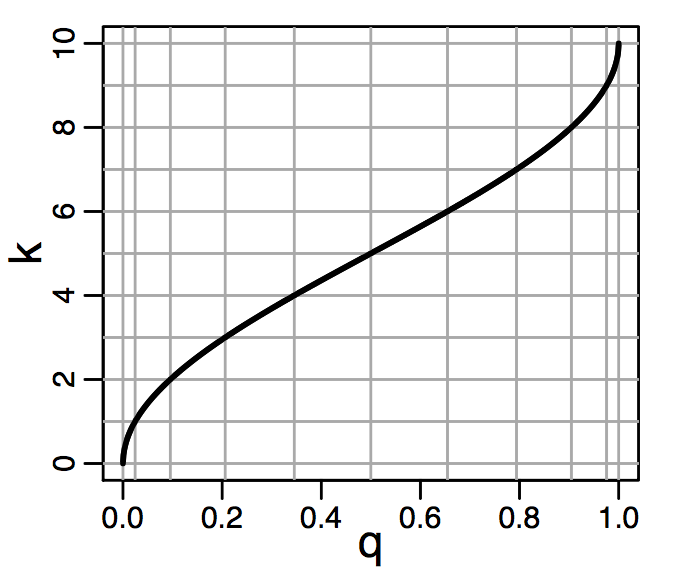
这个是映射函数在q=0或者q=1斜率很大,q=0.5附近斜率很小,所以可以保证 可以保证q=0或者q=1的质心权重较小,进而保证q=0或者q=1附近的百分位计算精度更高。
两种TDigest算法在将最新的point加入当前质心时,都需要进行权重的比较,如果当前point的权重+当前质心的权重 < 当前质心的最大权重,就加入的那个前质心,否则就根据当前point新建质心。
由于多个质心可以根据加权平均合并为一个质心,所以多个TDigest是可以合并的,即TDigest使符合结合律的,所以TDigest很容易用MapReduce计算。
TalkCody 欢迎 Star&共建
欢迎关注微信公众号
